
Μια σελίδα για τον
Πυθαγόρα και τους Πυθαγόρειους
Κωνσταντίνα Ζορμπαλά
Συγκέντρωση και παρουσίαση υλικού:
Αντώνης Τσολομύτης
•••
υπό συνεχή διαμόρφωση
•••
 |
Μια σελίδα για τον
Πυθαγόρα και τους Πυθαγόρειους
|
Πολλά έχουν λεχθεί και γραφτεί για τον Πυθαγόρα. Ποιος ήταν και τι ήταν ο Πυθαγόρας; Ήταν μαθηματικός, φιλόσοφος; Ήταν θαυματοποιός, ήταν θρησκευτικός αναμορφωτής; Ποιος είναι ο θρύλος και ποια είναι τα πραγματικά γεγονότα; Ποιες είναι οι μυθοπλασίες και ποια η ιστορία; Για να αναγνωρίσουμε το ιστορικό πρόσωπο πρέπει να καταφέρουμε να τα διαχωρίσουμε. Κείμενα Πυθαγορείων στην προσωκρατική εποχή δεν είναι γνωστά, οι πληροφορίες γίνονται πιο συγκεκριμένες, πιο ξεκάθαρες και πιο πολλές όσο περισσότερο πλησιάζουμε στα χρόνια μας. Όπως αναφέρει ο E. Zeller ήδη από τα τέλη του 19ου αιώνα, όσο απομακρυνόμαστε χρονικά από την εποχή του Πυθαγόρα, τόσο παρατηρούμε να πληθαίνουν οι πληροφορίες γύρω από τον Πυθαγόρα, τη ζωή και τη φιλοσοφία του.[Mattéi1995, σελ 1]
Για τη ζωή του έχουμε πληροφορίες από τους τελευταίους Πυθαγόρειους του 4ου αιώνα πριν την αρχή της χριστιανικής χρονολόγησης (στο εξής: παχχ) τον Αριστόξενο από τον Τάραντα (354–300 παχχ), μαθητή του Αριστοτέλη, που παρουσίασε τις απόψεις μιας συγκεκριμένης ομάδας των Πυθαγορείων και έχει γράψει τα «Περί του Πυθαγορικού βίου», «Περί Πυθαγόρου και των γνωρίμων αυτού», «Πυθαγορικές αποφάσεις», το Δικαίαρχο από τη Μεσσήνη (370–300 παχχ), που έζησε στην ίδια περιοχή που έζησαν οι Πυθαγόρειοι, και συνέλεξε όποια μαρτυρία υπάρχει σχετικά με τους Πυθαγορείους, τον Τίμαιο από το Ταυρομένιο (μέσα 4ου αιώνα παχχ), τον Ηρακλείδη τον Ποντικό (388–310 παχχ), μαθητή του Πλάτωνα (4ος αιώνας παχχ) που έγραψε τα «Περί Πυθαγορείων», «Περί της άπνου», «Περί δικαιοσύνης», «Αβαρις».
Επιπλέον πληροφορίες για τον Πυθαγόρα και τα μαθηματικά του έχουμε στα έργα του Αριστοτέλη (384–322 παχχ) «Μετά τα Φυσικά» και «Τέχνη Ρητορική». Υπάρχουν και τα έργα «Προς τους Πυθαγορείους», «Περί των Πυθαγορείων», «Συναγωγή των Πυθαγορικών», «Περί Πυθαγορικής Φιλοσοφίας» και «Πυθαγορικός», για τα οποία δεν γνωρίζουμε με σιγουριά εάν πρόκειται για διαφορετικά έργα ή όχι.
Υπάρχουν επίσης τρεις βιογραφίες του Πυθαγόρα, του Διογένη Λαέρτιου (3ος αιώνας μαχχ) «Πυθαγόρου βίος», του Πορφύριου (3ος–4ος αιώνας μαχχ, νεοπλατωνικός φιλόσοφος) «Περί του Πυθαγορικού Βίος» και του Ιάμβλιχου (3ος–4ος αιώνας μαχχ). Σχετικά με τις τρεις αυτές βιογραφίες του Πυθαγόρα (Διογένη, Πορφύριου, Ιάμβλιχου) ο καθηγητής φιλοσοφίας Θεόφιλος Βέικος γράφει: «Τα κείμενα αυτά … είναι τόσο αναξιόπιστα, ώστε να αναρωτιόμαστε πώς και από ποιες πηγές προέκυψαν όλα αυτά τα παράξενα πράγματα πυθαγορισμού, πλατωνισμού, αριστοτελισμού και στωϊκισμού», διαπιστώνοντας επιπλέον ότι «παρουσιάζεται το φαινόμενο πως οι πληροφορίες γίνονται πιο λεπτομερείς όσο απομακρυνόμαστε χρονικά από τον Πυθαγόρα» για να καταλήξει ότι είναι «δυσχερής μια συνεπής και θεμελιωμένη ανασυγκρότηση της σκέψης του ιστορικού Πυθαγόρα και εκείνης των πρώτων μαθητών του».[Βεΐκος1985, σελ. 139]
Υπάρχουν όμως και μεμονωμένες μαρτυρίες, συζητήσεις και ανέκδοτα, που βρίσκονται χρονικά πολύ κοντά στον Πυθαγόρα. Δεν πρόκειται για προσπάθειες να καταγραφεί η ζωή και φιλοσοφία του Πυθαγόρα και των μαθητών του, όπως οι προηγούμενες πηγές. Από αυτήν την άποψη θα μπορούσε κανείς να τις χαρακτηρίσει τις πιο αξιόπιστες πηγές.
Σε αυτούς τους συγγραφείς ανήκουν ο Ξενοφάνης, ο Ηράκλειτος (6oς–5ος αιώνας παχχ), που ήταν σύγχρονοι του Πυθαγόρα, ο Επίχαρμος (5ος αιώνας παχχ), ο Εμπεδοκλής (495–435 παχχ, που ήταν πυθαγόρειος), κάπως αργότερα ο Ηρόδοτος (485–415 παχχ), ο Πλάτωνας (427–347 παχχ) και ο Ισοκράτης (436–338 παχχ). Μεγάλης σημασίας είναι τα έργα του Εμπεδοκλή και εφόσον είναι αυθεντικά τα έργα του Πυθαγόρειου Φιλόλαου (470–385 παχχ).
|
Ο Ηράκλειτος αμφισβήτησε με έντονο τρόπο τον Πυθαγόρα, «η πολυμάθεια δεν διδάσκει να έχει κανείς μυαλό. Θα είχε άλλωστε διδάξει τον Ησίοδο και τον Πυθαγόρα» για να τον χαρακτηρίσει στη συνέχεια «κοπίδων αρχηγό» δηλαδή αρχηγό των απατεώνων. Ο Ηρόδοτος τον χαρακτηρίζει ως «έναν σημαντικό σοφιστή», δηλαδή δάσκαλο της σοφίας. Τον χαρακτηρίζει όμως και λογοκλόπο σε βάρος των Αιγυπτίων που πρώτοι θεώρησαν τη ψυχή αθάνατη και περαστική από σώμα σε σώμα. Αντίθετα ο Εμπεδοκλής: «Ανάμεσα σ᾽ εκείνους ζούσε ένας άντρας έξοχης γνώσης που απόχτησε τον μέγιστο πλούτο του πνεύματος και έγινε δημιουργός ποικίλων παρά σοφών έργων. Και κάθε φορά που επιστράτευε όλες τις πνευματικές του δυνάμεις έβλεπε εύκολα κάθε ένα απ᾽ όλα τα πράγματα που είχε δει σε διάστημα δέκα και είκοσι γενεών ανθρώπων ζωής».[Βεΐκος1985, σελ. 135] |
 Pythagoras and the fisherman (1662).[πηγή] Πίνακας του Ιταλού ζωγράφου Salvatore Rosa (1615–1673), βρίσκεται στη Gemaldegalerie του Βερολίνου. |
Τα στοιχεία για την χρονολογία και τη ζωή του Πυθαγόρα είναι εξαιρετικά αντιφατικά. Σύμφωνα με την παράδοση γεννήθηκε γύρω στο 570 παχχ και έζησε:[Fritz1963, σελ. 179,180]
Μετά από μια διεξοδική μελέτη των πηγών ο μελετητής της ζωής και του μαθηματικού έργου του Πυθαγόρα, Kurt von Fritz καταλήγει:[Fritz1963, σελ 185]
Η Πυθαγόρεια Σχολή θεώρησε ότι μέσα από τα Μαθηματικά μπορούμε να καταλάβουμε την οργάνωση και τη λογική που διέπει τον κόσμο. Συνέλαβε μάλιστα ολόκληρο τον κόσμο ως αρμονία και αριθμό. Θεώρησε ότι η τάξη του σύμπαντος μπορεί να εκφραστεί με αριθμητικές σχέσεις.
|
Οι Μιλήσιοι πριν από τον Πυθαγόρα είχαν προσπαθήσει να βρουν υλικά αίτια για να εξηγήσουν τον κόσμο. Ο Θαλής, προσωκρατικός φιλόσοφος του 6ου παχχ και ιδρυτής της Ιωνικής Σχολής στη Μίλητο, θεωρούσε ότι η αρχή του κόσμου είναι το νερό. Ήταν αυτός, σύμφωνα με μια αναφορά του Ευδήμου, που έθεσε τις βάσεις για την ανάπτυξη της θεωρητικής σκέψης στα Μαθηματικά. Με τον Πυθαγόρα γίνεται η απομάκρυνση από υλικά αίτια για την κατανόηση του κόσμου σε νοητικά αίτια και αρχές, όπως είναι ο Αριθμός. Σύμφωνα με τον W. Burkert στο έργο του «Weisheit und Wissenschaft. Studien zu Pythagoras, Philolaos und Platon», το νέο που έφεραν οι Πυθαγόρειοι, ήταν ότι έκαναν τα Μαθηματικά βάση της Φιλοσοφίας.[Burkert1962, σελ 391] |
 Pythagoras Emerging from the Underworld (1662).[πηγή] Πίνακας του Ιταλού ζωγράφου Salvatore Rosa (1615–1673). Βρίσκεται στο μουσείο Kimbell Art στο Τέξας των ΗΠΑ. |
Πολλοί ερευνητές του Πυθαγορισμού[Mattéi1995, σελ 78] βλέπουν ότι είναι πολύ πιθανόν η ανάμειξη των γνήσια πυθαγόρειων δογμάτων και των αριθμητικών εικοτολογικών θεωρήσεων της Ακαδημίας του Πλάτωνα να ξεκινά με τη σύνοψη του χαμένου συγγράμματος «Περί Πυθαγορείων Αριθμών» του Σπευσίππου, διαδόχου του Πλάτωνα στη σχολή. Αυτή η ανάμειξη δεν μας επιτρέπει να δούμε ξεκάθαρα εάν ο Πλάτων πυθαγορίζει ή αν αντίθετα οι Νεοπυθαγόρειοι και Νεοπλατωνιστές πλατωνίζουν.[Mattéi1995, σελ 78] Τελικά όποια και να είναι η αλήθεια, η ιστορική έρευνα καταλήγει ότι ο πυθαγορισμός απέδιδε μεγάλη σημασία στην έννοια του Αριθμού, νοούμενου ως θετικού ακεραίου. Όπως χαρακτηριστικά αναφέρεται «το αρχέγονο γνώρισμα του πυθαγορισμού έγκειται στην υπέρτατη εξουσία του Αριθμού».[Mattéi1995, σελ 78]
Ο Αριστοτέλης (384–322 παχχ) που αποτελεί την κύρια πηγή μας για τον Πυθαγορισμό αναφέρεται σε πολλά σημεία του έργου του στους Πυθαγόρειους και τη σχέση τους με τον Αριθμό. Διαβάζουμε στα «Μετά τα Φυσικά» (Μ.τ.φ.) του Αριστοτέλη:
| Τι σημαίνει ότι … ο αριθμός είναι η ουσία των πραγμάτων; τα πράγματα παράγονται από αριθμούς; ολόκληρο το σύμπαν κατασκευάζεται από αριθμούς; όλα τα όντα είναι τέλεια απεικόνιση του αριθμού; |
|
Να πούμε σ᾽ αυτό το σημείο ότι σε
αντίθεση με την αντίληψη που έχουμε εμείς για τους
αριθμούς, οι Πυθαγόρειοι δεν έβλεπαν τους αριθμούς ισότιμα
μεταξύ τους. Ο κάθε αριθμός είχε μια συγκεκριμένη
λειτουργία. Η αρχή της Πυθαγόρειας Θεωρίας Αριθμών
(αν μπορούμε να την ονομάσουμε έτσι)
συνίσταται στην ταξινόμησή
τους σε καθορισμένες κατηγορίες με βάση το υπόλοιπο της
διαίρεσης με τον αριθμό |
 Pythagoras [πηγή] Πίνακας της σχολής του Ιταλού ζωγράφου Luca Giordano (1634–1705). |
Με αυτήν την επιλογή ως αφετηρία οι Πυθαγόρειοι διαιρούσαν τον αριθμό, η ουσία του οποίου είναι η μονάδα, σε περιττούς και άρτιους. Οι περιττοί είναι πεπερασμένοι, περιορισμένοι. Οι άρτιοι είναι απεριόριστοι, άπειροι.
Ο περιττός δεν μπορεί να διαιρεθεί σε δύο
ίσα μέρη, για παράδειγμα ο
Αντίθετα ο άρτιος μπορεί να διαιρεθεί σε δύο ίσα μέρη, συνεπώς δεν περιορίζεται από τη μονάδα, είναι άπειρος. Eπειδή ο άρτιος μπορεί να διαιρεθεί σε δύο μέρη χαρακτηρίζεται «θηλυκός», ενώ ο περιττός χαρακτηρίζεται «αρσενικός» αριθμός.
Ο περιττός επειδή έχει αρχή, μέση και τέλος,
όπως στο προηγούμενο παράδειγμα ο
Υπάρχει επιπλέον ένας φυσικός δεσμός μεταξύ περιττών και αρτίων: Δεδομένου ότι κάθε άρτιος διαιρείται σε δύο ίσα μέρη, τα μέρη αυτά μπορούν να χωριστούν από μια ευθεία που προεκτείνεται επ᾽ αόριστον από τις δύο πλευρές. (για την σχετική αναπαράσταση των αρτίων και περιττών: [Heidel1901, σελ 395])

Αντιθέτως ο περιττός εισάγει μια διάμεση μονάδα που τον περιορίζει.
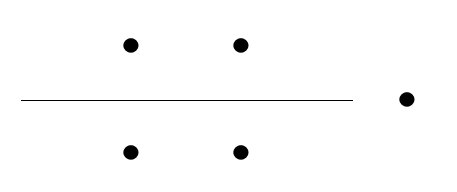
Η θεωρία των Αρτίων και Περιττών
στα
|
Περνάμε στους «παραστατικούς» αριθμούς,
αριθμούς που παριστάνουν ένα τρίγωνο, ένα τετράγωνο, ένα
πεντάγωνο κλπ. Ποιοι είναι και πώς παράγονται; Είναι
αριθμοί που δημιουργούν γεωμετρικά σχήματα και άρα
δημιουργούν το γεωμετρικό χώρο; |
 Pythagoras–The beginnings of Science (1906). [πηγή] Πίνακας του Veloso Salgado (1864–1945). Βρίσκεται στην Ιατρική Σχολή του Νέου Πανεπιστημίου της Λισσαβώνας. |
Οι τέσσερις πρώτοι αριθμοί συγκροτούν στην
Πυθαγόρεια Φιλοσοφία το «ιερό τρίγωνο της Τετράδας» (Τετρακτύς
όπως λέγεται), το άθροισμα της οποίας είναι η Δεκάδα (
Με άλλα λόγια οι τρεις διαστάσεις του χώρου έχουν αντιστοιχία σε αριθμούς. Εφ᾽ όσον τα πάντα είναι αριθμός μπορεί να αποδειχθεί ότι ο χώρος έχει αριθμητική δομή, αρκεί να εξομοιωθούν οι αριθμοί με γεωμετρικά σημεία. Παραθέτουμε μερικά παραδείγματα:
Αν στον αριθμό
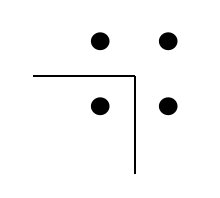
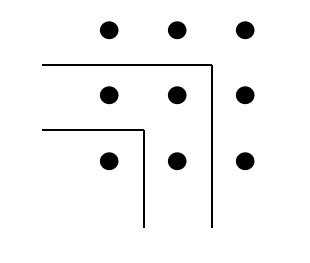
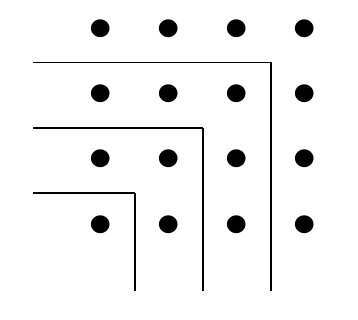
Με βάση τα παραπάνω οι Πυθαγόρειοι «μας
λένε» πως το άθροισμα περιττών αριθμών είναι ένας αριθμός που
έχει σχήμα τετραγώνου, «τετράγωνος» αριθμός όπως τον λέγανε.
Εμείς σήμερα γράφουμε
Ας πάρουμε ένα άλλο παράδειγμα, το άθροισμα
αρτίων αριθμών: Αν στον αριθμό
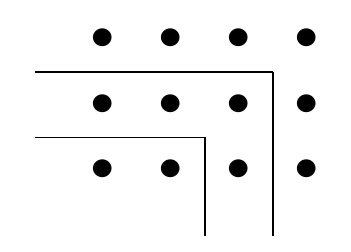
Με άλλα λόγια, οι Πυθαγόρειοι «μας λένε» ότι
το άθροισμα αρτίων αριθμών,
Ένα άλλο παράδειγμα είναι το άθροισμα αρτίων
και περιττών αριθμών. Αν προσθέσουμε άρτιους και περιττούς κατά
αύξουσα σειρά, δηλαδή

Αφού ο χώρος εξομοιώθηκε με αριθμούς, περνάμε στις ιδιότητες του γεωμετρικού χώρου.
Ακολουθώντας τον Πρόκλο μπορούμε να συγκεφαλαιώσουμε ως εξής τις ανακαλύψεις των Πυθαγορείων στη γεωμετρία:[Mattéi1995, σελ 89–101]
| πέρας |
↔ |
άπειρον |
| περιττόν |
↔ |
άρτιον |
| εν |
↔ |
πλήθος |
| δεξιόν |
↔ |
αριστερόν |
| άρρεν |
↔ |
θήλυ |
| ηρεμούν |
↔ |
κινούμενον |
| ευθύ |
↔ |
καμπύλον |
| φως |
↔ |
σκότος |
| αγαθόν |
↔ |
κακόν |
| τετράγωνον |
↔ |
ετερόμηκες |
Ο Αριστοτέλης αποδίδει αυτόν τον πίνακα στον Αλκμαίωνα, χωρίς να μπορεί να πει αν ο Αλκμαίων τον δανείστηκε από τους Πυθαγόρειους ή οι Πυθαγόρειοι από τον Αλκμαίωνα, ή απλώς αν ο Αλκμαίων ήταν κι αυτός Πυθαγόρειος. Το γεγονός πάντως είναι ότι ο πίνακας καταφάσκει και πάλι στην πρόταση ότι «τα αντίθετα είναι οι αρχές των όντων».[Mattéi1995, σελ 85]Πιστεύεται ότι ο Πυθαγόρας ανακάλυψε το περιβόητο θεώρημα, το «πυθαγόρειο», που επίσης αποκαλείται «θεώρημα των τριών τετραγωνικών». Σύμφωνα με την παράδοση, ο Πυθαγόρας γιόρτασε την ανακάλυψή του θυσιάζοντας βόδια προς τιμήν των Μουσών. Σχετικά με το γνωστό μας Πυθαγόρειο θεώρημα θα επανέρθουμε στη συνέχεια.
Πότε και πώς ανακαλύφθηκε η ασυμμετρία δεν μπορούμε να πούμε με βεβαιότητα. Ο Πρόκλος αποδίδει την ανακάλυψη της ασυμμετρίας στον ίδιο τον Πυθαγόρα. Πολύ πιθανόν ήταν ο Πάππος που σε ένα σχόλιό του αναφέρει ότι η θεωρία των αρρήτων ξεκινά στη σχολή του Πυθαγόρα.
|
Σύμφωνα με τον Αριστοτέλη και τον
Πρόκλο, οι Πυθαγόρειοι ανακάλυψαν την ασυμμετρία της
διαγωνίου του τετραγώνου, δηλαδή το πρώτο άρρητο μέγεθος.
Οδηγήθηκαν σε αυτή την ανακάλυψη από την διαπίστωση της
ύπαρξης ευθύγραμμων τμημάτων που δεν έχουν κοινό μέτρο.
Σύμφωνα με τον van der Waerden οι Πυθαγόρειοι είχαν τα
απαραίτητα αποδεικτικά μέσα από την θεωρία των αρτίων και
περιττών για την ασυμμετρία της διαγωνίου.[Waerden1979, σελ 399] Σύμφωνα όμως με
τον Kurt von Fritz η πρώτη ασυμμετρία που ανακαλύφθηκε δεν
είναι αυτή της διαγωνίου του τετραγώνου αλλά της διαγωνίου
του κανονικού πενταγώνου. Ο van der Waerden θεωρεί αυτό
πιθανό αλλά όχι
σίγουρο.[Waerden1979, σελ 399] |
 Pythagoras [πηγή] Πίνακας της σχολής του Ιταλού ζωγράφου Luca Giordano (1634–1705). Βρίσκεται στο Εθνικό Μουσείο στο Βρότσλαβ της Πολωνίας |
Η αρχαιότερη σωζόμενη αναφορά περιέχεται στα «Αναλυτικά Πρότερα» του Αριστοτέλη, σύμφωνα με την οποία, εάν υποθέσουμε ότι η πλευρά και η διαγώνιος του τετραγώνου είναι σύμμετρες, τότε καταλήγουμε στην αντίφαση ότι τα άρτια γίνονται ίσα με τα περιττά, κάτι που οδηγεί στο συμπέρασμα ότι υπάρχει ασύμμετρη σχέση μεταξύ τους. Αυτή η «απόδειξη» προϋποθέτει όμως τη γνώση της αρρητότητας.
Το ίδιο ισχύει και στην απόδειξη που
παρουσιάζεται στα
Μια εκδοχή απόδειξης έχει διατυπωθεί από τον Oscar Becker.
Η ανακατασκευή του Becker μπορεί να περιγραφεί ως εξής: [Χριστιανίδης2003, σελ 77]
Οι Πυθαγόρειοι μελέτησαν το πρόβλημα της
εύρεσης ορθογωνίων τριγώνων με πλευρές ακέραιους αριθμούς. Από
αυτό μπορούμε να υποθέσουμε ότι θα ενδιαφέρθηκαν να εξετάσουν
εάν υπάρχουν ισοσκελή τρίγωνα που να ανήκουν σε αυτήν την
κατηγορία. Σε ένα ισοσκελές τρίγωνο με α την υποτείνουσα
και β τη μια από τις ίσες κάθετες πλευρές, ισχύει ότι
Στην περίπτωση I από το τετράγωνο P καταλήγουμε μετά από έναν αριθμό διαιρέσεων σε ένα περιττό τετράγωνο P ', ενώ σε σχέση με το Q μετά από έναν αριθμό διαιρέσεων κατλήγουμε ή στην περίπτωση Q ' το οποίο μπορεί να είναι άρτιο (περίπτωση ΙΑ) ή περιττό (περίπτωση ΙΒ). Και στις δύο περιπτώσεις προκύπτει ότι ένας περιττός αριθμός είναι ίσος με το διπλάσιο ενός αριθμού άρτιου τη μια φορά και περιττού στην άλλη, κάτι το οποίο είναι αδύνατο.
| A) |
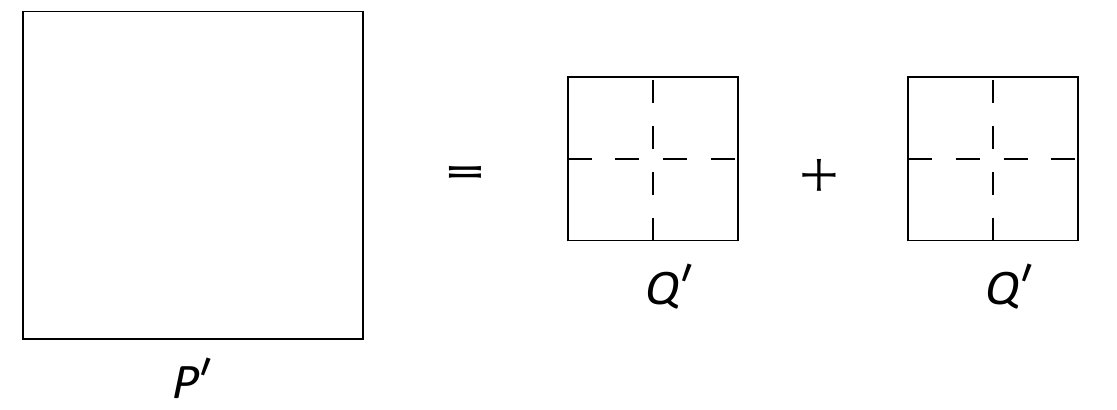 |
| B) |
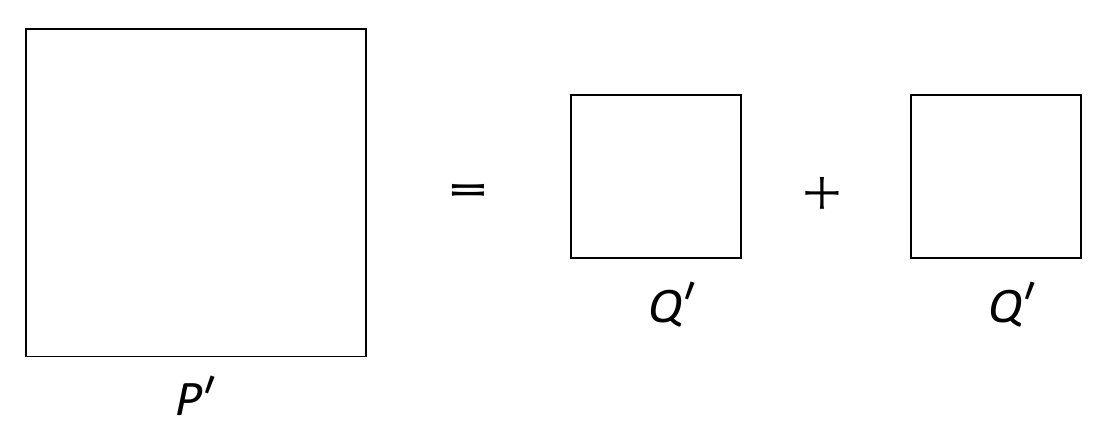 |
Στην περίπτωση II καταλήγουμε να
έχουμε ένα άρτιο τετράγωνο Ρ ', που είναι ίσο με το
διπλάσιο ενός περιττού τετραγώνου Q ''. Το Ρ ''
επειδή είναι άρτιο μπορεί να χωριστεί σε τέσσερα μικρότερα
τετράγωνα, καθένα από τα οποία είναι ίσο με r και
επομένως καταλήγουμε
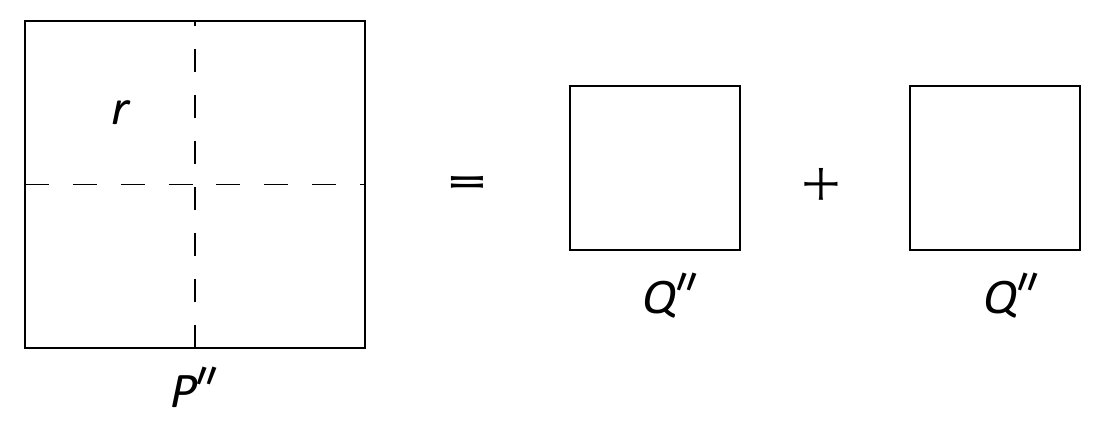 |
οπότε |
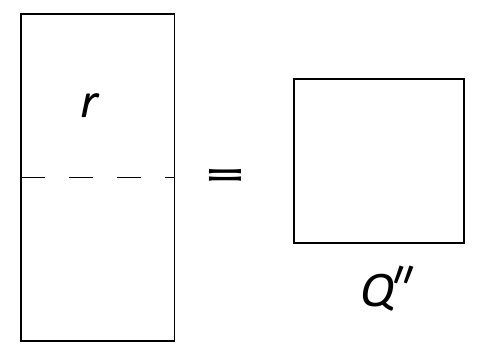 |
Με βάση τα παραπάνω καταλήξαμε ότι δεν
υπάρχουν ισοσκελή ορθογώνια τρίγωνα με πλευρές ακέραιους, με
άλλα λόγια ότι η εξίσωση
Πάμπολλες είναι οι αναφορές, ότι ο Πυθαγόρας απέδειξε το γνωστό θεώρημα. Επίσης είναι πολύ συχνή η αναφορά ότι ο Πυθαγόρας ανακάλυψε το πυθαγόρειο θεώρημα. Που τελειώνει ο μύθος, που αρχίζει η ιστορική αλήθεια; Που μας οδηγούν οι πηγές;
Αυτό που σίγουρα γνωρίζουμε από πηγές είναι ότι
οι Αιγύπτιοι έκαναν εμπειρική χρήση αυτής της σχέσης
σε κάθε τρίγωνο ξεχωριστά, χωρίς να υπάρχει από μεριάς τους
μια γενική διατύπωση έστω και σε πρωταρχική μορφή,
κάτι που οδηγεί αναπόφευκτα στο συμπέρασμα ότι δεν είχαν
διαμορφώσει την γεωμετρική έννοια του τριγώνου και πολύ
περισσότερο την έννοια της ιδιότητας ενός τριγώνου.
Γνωρίζουμε επίσης για τους
Βαβυλώνιους, ότι έκαναν συνεχή εφαρμογή της σχέσης σε μεμονωμένα
ορθογώνια τρίγωνα. Την πρώτη μαθηματική απόδειξη της ιδιότητας
βρίσκουμε στα
Για τη σύνδεση του Πυθαγόρα με το σχετικό θεώρημα υπάρχουν πολλές αναφορές από των αρχαιοτάτων χρόνων. Ας τις δούμε: (Για τις παραπομπές και μεταφράσεις βλέπε [Σωτηρίου2017].)
Ξεκινάμε με τον Κικέρωνα τον 1ο αιώνα παχχ:[ό.π., σελ. 33]
|
«Είναι αλήθεια ότι υπάρχει μια ιστορία κατά την οποία ο Πυθαγόρας θυσίασε ένα βόδι προς τιμήν των Μουσών, όταν έκανε μια νέα ανακάλυψη στη γεωμετρία. Αλλά εγώ δεν την πιστεύω, επειδή (ο Πυθαγόρας) αρνούνταν να προβεί σε θυσία, ακόμα και χάριν του Δήλιου Απόλλωνα, για να μην πασπαλιστεί με αίμα ο βωμός.» |
Ο Κικέρωνας αναφέρεται σε μια ιστορία που γνωρίζει σύμφωνα με την οποία ο Πυθαγόρας έκανε μια ανακάλυψη στη γεωμετρία, χωρίς να λέει ποια είναι αυτή. Δεν τη γνωρίζει; Είναι κάτι αυτονόητο που δεν χρειάζεται να το αναφέρει; Από τις αναφορές που θα ακολουθήσουν, μάλλον δεν είναι ξεκάθαρο. Επιπλέον δεν θεωρεί ότι ο Πυθαγόρας έκανε θυσία μετά από αυτήν την ανακάλυψη.
Η μαρτυρία του Βιτρούβιου τον 1ο αιώνα παχχ είναι πιο συγκεκριμένη:[ό.π., σελ. 34]
|
«Ο Πυθαγόρας επέδειξε τη μέθοδο κατασκευής ορθογωνίου τριγώνου, χωρίς τη χρήση εργαλείων που κατέχουν οι τεχνίτες. Αυτό που εκείνοι μόλις καταφέρνουν να πετύχουν, ακόμη και με μεγάλο κόπο, μπορεί να γίνει πολύ εύκολα με τους κανόνες του. Ας παρθούν τρεις ράβδοι, μία ίση με τρία πόδια, μία με τέσσερα και μία με πέντε. Και ας ενωθούν, έτσι ώστε το άκρο της κάθε μίας να αγγίζει αυτό της άλλης. Τότε θα σχηματίσουν ένα τρίγωνο, του οποίου μία γωνία είναι ορθή. Και αν σχεδιαστούν τρία τετράγωνα που να έχουν πλευρά την κάθε ράβδο, τότε αυτό των τριών ποδιών θα έχει έκταση εννέα πόδια, των τεσσάρων δεκαέξι και των πέντε είκοσι πέντε. Ώστε, αν οι αριθμοί των ποδιών, τα περιέχοντα στα τετράγωνα των τριών και τεσσάρων προστεθούν, θα ισούνται με αυτόν των ποδιών, τα περιέχοντα στο τετράγωνο των πέντε. Όταν ο Πυθαγόρας ανακάλυψε ετούτο το δεδομένο, δεν είχε την παραμικρή αμφιβολία ότι τον βοήθησαν οι Μούσες, γι’ αυτό και εξέφρασε την ευγνωμοσύνη του προς εκείνες με μια θυσία. Αυτή η πρόταση είναι χρήσιμη σε πολλές περιπτώσεις, ιδιαίτερα στη μέτρηση, και όχι λιγότερο στην κατασκευή κτηριακών σκαλών, έτσι ώστε κάθε σκαλοπάτι να έχει το σωστό ύψος.» |
Σύμφωνα με τον Βιτρούβιο η κατασκευή που
έκανε ο Πυθαγόρας και η οποία αποτέλεσε αφορμή για θυσία, αφορά
την κατασκευή ενός ορθογωνίου τριγώνου με πλευρές
Στον Πλούταρχο (1ο–2ο αιώνα μαχχ) βρίσκουμε την παρακάτω αναφορά:[ό.π., σελ. 36]
|
«… και ο Πυθαγόρας θυσίασε ένα βόδι λόγω των σχημάτων του, όπως λέει ο Απολλόδωρος όταν ο `Πυθαγόρας βρήκε το περίφημο σχήμα, προχώρησε σε λαμπρή θυσία,' είτε αυτό ήταν το περί του τετραγώνου της υποτείνουσας (κάθε ορθογωνίου τριγώνου) που ισούται με αυτά (των πλευρών) οι οποίες περιέχουν την ορθή (γωνία), είτε το πρόβλημα που αφορά την παραβολή χωρίων.» |
Ο Πλούταρχος παραπέμπει στον Απολλόδωρο για την κατασκευή του Πυθαγόρα, αλλά δεν είναι σίγουρος για το αν η κατασκευή αφορούσε τη σχέση στο ορθογώνιο τρίγωνο ή το πρόβλημα της παραβολής χωρίων. Σε άλλο κείμενό του αναφέρει:[ό.π.]
|
«Διότι μεταξύ των σημαντικότερων γεωμετρικών θεωρημάτων, μάλλον δε προβλημάτων, είναι το εξής: δοθέντων δύο (σχημάτων), να παρεμβληθεί ένα τρίτο που να είναι ίσο με το πρώτο και όμοιο με το δεύτερο. Λέγεται ότι εξαιτίας αυτής της ανακάλυψης, ο Πυθαγόρας προχώρησε σε θυσία· διότι αυτό είναι γλαφυρότερο και μουσικότερο του θεωρήματος που επίσης απέδειξε και που αφορά την ισότητα του τετραγώνου της υποτείνουσας (κάθε ορθογωνίου τριγώνου) με αυτά (των πλευρών) που περιέχουν την ορθή γωνία.» |
Σε αυτό το κομμάτι γίνεται ξεκάθαρη αναφορά σε γεωμετρικό θεώρημα. Ο Πλούταρχος φαίνεται πιο σίγουρος και ισχυρίζεται ότι αφορμή για την θυσία αποτέλεσε η επίλυση του προβλήματος της παραβολής. Ισχυρίζεται επίσης ότι ο Πυθαγόρας απέδειξε και τη σχέση στο ορθογώνιο τρίγωνο. Συνεπώς σύμφωνα με τον Πλούταρχο ο Πυθαγόρας απέδειξε τόσο το θεώρημα στα ορθογώνια τρίγωνα όσο και το πρόβλημα της παραβολής.
Και ο Αθηναίος (2ο–3ο αιώνα μαχχ) παραπέμπει στον Απολλόδωρο αλλά θεωρεί ότι αφορμή για τη θυσία είναι η κατασκευή των τετραγώνων στις πλευρές του ορθογώνιου τρίγωνου και η ισότητα του τετραγώνου της υποτείνουσας με το άθροισμα των άλλων δύο:[ό.π., σελ. 37]
|
«Ο Απολλόδωρος δε ο αριθμητικός λέει ότι (ο Πυθαγόρας) προέβη σε θυσία εκατόμβης όταν βρήκε πως σε κάθε ορθογώνιο τρίγωνο το τετράγωνο της υποτείνουσας είναι ίσο προς αυτά (των πλευρών) που περιέχουν την ορθή γωνία· όταν ο ξακουστός Πυθαγόρας βρήκε το περίφημο σχήμα, προχώρησε στη γνωστή θυσία βοδιού.» |
Το ίδιο ακριβώς χωρίο το βρίσκουμε στο Διογένη Λαερτίου τον 3ο αιώνα μαχχ:[ό.π., σελ. 38]
|
«Ο Απολλόδωρος δε ο λογιστικός λέει ότι (ο Πυθαγόρας) προέβη σε θυσία εκατόμβης, όταν βρήκε πως σε κάθε ορθογώνιο τρίγωνο το τετράγωνο της υποτείνουσας είναι ίσο προς αυτά (των πλευρών) που περιέχουν (την ορθή γωνία). Και υπάρχει το εξής επίγραμμα: όταν ο ξακουστός Πυθαγόρας βρήκε το περίφημο σχήμα, προχώρησε στη γνωστή θυσία βοδιού.» |
Ο Πορφύριος τον 3ο αιώνα μαχχ θα αναφερθεί σε θυσία ομοιώματος και σε ανακάλυψη σχέσης και όχι κατασκευή σχήματος:[ό.π.]
|
«Προχώρησε κάποτε σε θυσία ενός ομοιώματος βοδιού από ζυμάρι, σύμφωνα με εκείνους που γνωρίζουν καλύτερα, όταν βρήκε πως σε κάθε ορθογώνιο (τρίγωνο) το τετράγωνο της υποτείνουσας ισούται προς αυτά των (πλευρών) που περιέχουν (την ορθή γωνία).» |
Στα σχόλια του Νεοπλατωνιστή Πρόκλου τον 5ο
αιώνα μαχχ πάνω στην πρόταση των
|
«Αν λάβουμε υπόψιν αυτούς που εξιστορούν τα αρχαία πεπραγμένα, το θεώρημα τούτο αποδίδεται στον Πυθαγόρα και λέγεται ότι θυσίασε ένα βόδι λόγω της ανακάλυψης του. Εγώ δε, αν και θαυμάζω τους πρώτους που κατέδειξαν την αλήθεια αυτού του θεωρήματος, θαυμάζω ακόμα περισσότερο τον συγγραφέα των Στοιχείων, όχι μόνο επειδή εξασφάλισε τούτη διά της διαυγέστερης απόδειξης, αλλά επειδή έκανε το ίδιο και για τη γενικότερη του μορφή, στο έκτο βιβλίο, χρησιμοποιώντας αναμφισβήτητα επιστημονικά επιχειρήματα.» |
Ο Πρόκλος αποφεύγει ουσιαστικά κάποιο αναλυτικό σχολιασμό στο τι έκανε ο Πυθαγόρας, λέει ότι οι προηγούμενοι σχολιαστές έχουν αναφερθεί στην ανακάλυψη του θεωρήματος από τον Πυθαγόρα και στη θυσία ενός βοδιού για να προχωρήσει αμέσως στο σχολιασμό της πρότασης από τον Ευκλείδη.
Απ᾽ όλες αυτές τις μαρτυρίες, φαίνεται ότι το έργο των συγγραφέων ήταν πολύ δύσκολο αφού είχαν να συσχετίσουν ένα τόσο σημαντικό θεώρημα με τον Πυθαγόρα, χωρίς όμως να έχουν επαρκείς πληροφορίες. Όλα σχεδόν τα κείμενα είναι βασισμένα στα λεγόμενα του Απολλοδώρου, ο οποίος αν είναι ο Απολλόδωρος ο Κυζικηνός (4ος αιώνας παχχ), τότε η ιστορία έχει προευκλείδειες ρίζες. Επίσης, οι συγγραφείς έπρεπε να αντιμετωπίσουν το θέμα της θυσίας, γεγονός που φάνταζε αδιανόητο αφού ερχόταν σε αντίθεση τόσο με τις διατροφικές συνήθειες της σχολής της οποίας ήταν ιδρυτής ο Πυθαγόρας, όσο και της πάγιας τακτικής που ακολουθούσε ο Πυθαγόρας, δηλαδή, να μην θανατώνει ζώα.[ό.π., σελ. 39 κ.ε.]
Οι τετραγωνισμοί των μηνίσκων του Ιπποκράτη του Χίου (470–410 παχχ), που χρησιμοποιεί στις αποδείξεις του ρητά διατυπωμένο ή εμμέσως εννοούμενο, το Πυθαγόρειο θεώρημα, μας οδηγεί στο συμπέρασμα ότι γύρω στο 430 παχχ, δηλαδή την εποχή της ακμής του Ιπποκράτη του Χίου, η γνώση του Πυθαγόρειου θεωρήματος είναι αναμφισβήτητη.[ό.π., σελ. 42 κ.ε.]
Οι πηγές αυτές που εξετάστηκαν δεν μπορούν να μας δώσουν ξεκάθαρη εικόνα για το ποιος ήταν αυτός που απέδειξε πρώτος το λεγόμενο Πυθαγόρειο Θεώρημα. Σύμφωνα με την προηγηθείσα ανάλυση, εκτιμάται ότι η αυθεντική απόδειξη του Πυθαγορείου Θεωρήματος προήλθε από τον κύκλο των Πυθαγορείων, κάπου ανάμεσα στα 450 και 430 παχχ.